Geometrically Frustrated Magnetism in the Heisenberg Pyrochlore Antiferromagnets AYb2X4 (A = Cd and Mg, X = S and Se)
Nakatsuji Group
Quantum magnetism in geometrically frustrated magnets has recently attracted great interest. In 3D systems, one of the most prominent examples is the spin ice [1], which is based on Ising spins with ferromagnetic (FM) coupling on the pyrochlore lattice. Recent studies have found that quantum melting of spin ice may lead to the formation of a quantum spin liquid state with emergent topological excitations [2]. On the other hand, various types of quantum magnetism have been discovered in the pyrochlore oxides having the non-Ising type ground Kramers doublet. An antiferromagnetic (AF) pyrochlore magnet with isotropic bilinear exchange coupling between nearest neighbor Heisenberg spins has been predicted to host an equally exotic magnetic ground state [3]. As one of the archetypes, Gd2Ti2O7 has attracted much attention and extensive studies have revealed frustrated magnetism with unconventional AF ordering [4].
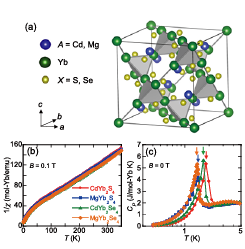
Fig. 1. (a) Crystal structure of the chalcogenide spinels AYb2X4 (A = Cd and Mg, X = S and Se). While the tetrahedrally coordinated nonmagnetic A sites form a diamond cubic sublattice, the magnetic Yb sites form a pyrochlore lattice with corner-sharing tetrahedra. Temperature dependence of (b) the inverse magnetic susceptibility 1/χ measured under 0.1 T and (c) the total specific heat CP at 0 T of the chalcogenide spinels AYb2X4.
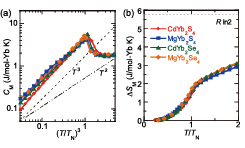
Fig. 2. (a) Full logarithmic plot of the magnetic specific heat CM vs. (T/TN)3 of the chalcogenide spinels AYb2X4 (A = Cd and Mg, X = S and Se). The dashed and two dot-dashed lines indicate the slopes for the T3 and T2 laws, respectively. (c) T/TN dependence of the magnetic entropy ∆SM of the chalcogenide spinels AYb2X4.
However, other than Gd, most of the rare earth ions in the pyrochlore oxides are known to have a strong trigonal crystal electric field (CEF) that stabilizes either Ising or XY planar local symmetry. To develop a deep understanding of frustrated magnetism in Heisenberg pyrochlore antiferromagnets, we have focused on spinel type AF materials AR2X4, where the rare earth R forms the pyrochlore lattice with different coordination from the oxides and possesses a nearly cubic site symmetry that can lead to Heisenberg spins.
Experimental studies on polycrystalline samples of the Yb-based chalcogenide spinels AR2X4 (A = Cd and Mg, X = S and Se) [5] have revealed frustrated quantum magnetism due to antiferromagnetically coupled Heisenberg spins on the pyrochlore lattice [6]. As shown in Fig. 1(a), the AYb2X4 families have the spinel structure with the space group Fd3m. The Yb3+ forms the pyrochlore lattice with the six-fold chalcogen X2− coordination and the point symmetry is D3d. The CEF analysis indicates the Yb ground state has nearly Heisenberg spins with a strong quantum character of the ground-state doublet due to the mixing of important components including ±Jz = 1/2. Our low-temperature susceptibility (Fig. 1(b)) and specific heat (Fig. 1(c)) measurements have revealed that all the materials exhibit AF order at TN = 1.4 – 1.8 K, much lower temperatures than the AF exchange coupling scale of ~ 10 K. The magnetic specific heat CM shows a T3 dependence, indicating the gapless feature expected for a linearly dispersive Nambu-Goldstone mode in 3D systems [Fig. 2(a)]. Figure 2(b) indicates the temperature dependence of the entropy ∆SM = SM(T) − SM(0.4 K). The ∆SM at TN is strongly suppressed to ~30% of Rln2 due to the geometrical frustration. Muon spin rotation/relaxation (µSR) measurements have confirmed the commensurate and incommensurate ordered states in CdYb2S4 and MgYb2S4, respectively, and a small local field at the muon site, which indicate the significantly reduced size of the ordered moment in comparison with the bare moment size 1.33 μB/Yb, suggesting strong quantum fluctuations in the Yb-based chalcogenide spinels AYb2X4.
References
- [1] M. J. Harris et al., Phys. Rev. B 79, 2554 (1997); A. P. Ramirez et al., Nature 399, 333 (1999); M. J. P. Gingras and P. A. McClarty, Rep. Prog. Phys. 77, 056501 (2014).
- [2] S. Nakatsuji, Phys. Rev. Lett 96, 087204 (2006); J. -J. Wen et al., Phys. Rev. Lett. 118, 107206 (2017).
- [3] R. Moessner and J. T. Chalker., Phys. Rev. Lett. 80, 2929 (1998).
- [4] N. P. Raju et al., Phys. Rev. B 59, 14489 (1999); B. Javanparast et al., Phys. Rev. Lett. 114, 130601 (2015).
- [5] L. Pawlak et al., J. Magn. Magn. Mater. 76-77, 199 (1988); G. C. Lau et al., Phys. Rev. B 72, 054411 (2005).
- [6] T. Higo, K. Iritani, M. Halim, W. Higemoto, T. U. Ito, K. Kuga, K. Kimura, and S. Nakatsuji, Phys. Rev. B 95, 174443 (2017).
