Optical conductivity is one of fundamental dynamical correlation functions in solids and measures a metallicity. A few years ago, we numerically investigated optical conductivity near the Mott metal-insulator transition in the frustrated Hubbard model on a triangular lattice using a cluster dynamical-mean field theory (CDMFT). We found a singularity in its dc value and in contrast to general belief the corresponding critical exponent does not coincide with that of the order parameter [1]. Another important finding was that the vertex corrections are not so important in that case. The Mott transition is driven by strong correlation effects, which may suggest large vertex corrections. However, our numerical data exhibited only a minor contribution of theirs, and it is likely due to two characteristic features in this system. The first is that spin fluctuations depend little on wave vectors because of strong frustration. The second is that quasiparticle scatterings due to spin fluctuations do not depend so much on their position on the Fermi surface. We have performed a new study to examine if the vertex corrections are more pronounced in an unfrustrated system. To compare with the previous result, we particularly investigated the temperature region near an antiferromagnetic phase transition.

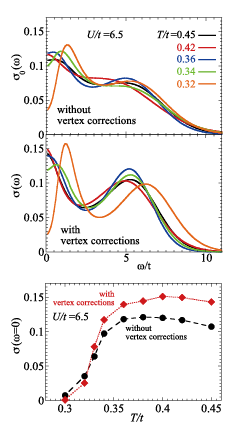
Fig. 1. (Top) Optical conductivity in the square-lattice Hubbard model at half filling. Units are the quantum conductance. (Bottom) Temperature dependence of dc conductivity in the same model.

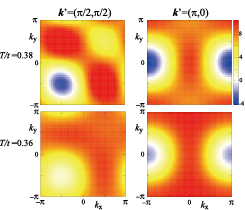
Fig. 2. Momentum dependence of the vertex function Γ that describes the process that a particle-hole pair with momentum and spin (k’, σ’) are scattered to another pair with (k, σ). Plotted is the charge part summed over σ and σ’ at Matsubara frequency ν_n =0. Dependences on temperature and k–k’ strongly vary with the initial momentum k’.

We have used a 4-site CDMFT approach for calculating optical conductivity σ(ω) in the square-lattice Hubbard model at half filling, and studied its temperature dependence both above and below the antiferromagnetic transition temperature T_N for the Coulomb repulsion U=6.5t. Here, t is the matrix element of nearest-neighbor hopping. A real antiferro long-range order is absent in two-dimensional systems, and our results correspond to quasi-two-dimensional systems. To implement the vertex corrections in the antiferromagnetic phase, we have derived a new formula based on our previous one for the paramagnetic phase. We have found that the vertex corrections change various important details in temperature and frequency dependence of conductivity near T_N. This point differs from our previous study on optical conductivity near the Mott transition in a frustrated triangular lattice.

General trends in the temperature evolution of σ(ω) are consistent with expected behaviors near the metal-insulator transition. In the high-temperature paramagnetic phase, σ(ω)has the Drude peak at ω=0 and also a broad peak around ω~U, which is related to excitations to the Hubbard bands. With lowering temperature, an antiferromagnetic phase transition occurs at T_N~0.34t, and σ(ω) changes its frequency dependence below T_N. While the incoherent peak continues to exist, now a dip appears at ω=0 and the low-energy peak shifts to ω~t. Top two panels in Fig. 1 compare σ(ω) with and without the vertex corrections. Most importantly, the vertex corrections enhance variations in the frequency dependence. The Drude peak and the high-ω broad peaks in the paramagnetic phase are both sharpened. This continues in the antiferromagnetic phase and the two peaks are both sharpened by the vertex corrections, whereas the dip at ω=0 is also enhanced. Another important discovery is the behavior in a temperature region just above T_N. As shown in the bottom panel in Fig. 1, dc conductivity decreases in this region with lowering temperature, which is a precursor of the transition. However, the electron excitation spectrum shows no pseudogap behavior and the Drude peak is pinned at ω=0. This temperature region appears before including the vertex corrections, but the corrections extends it quite wide. These are main results directly related to observable properties in experiments.

For better understanding of the vertex corrections, we have also carried out their detailed analysis. The vertex corrections are determined by the vertex function Γ and four single-electron Green's functions. As for the part of the Green's functions, we have found that their spin dependent components provide a dominant contribution in the antiferromagnetic phase. For Γ a predominant contribution is given by the scattering processes of polarization made of a particle on one sublattice and a hole on the other sublattice. We have also examined Γ’s momentum dependence. Results in the paramagnetic phase are shown in Fig. 2. In the antiferromagnetic phase, the charge vertex and spin vertex functions have similar momentum dependence but the sign is opposite. A large difference is found in Γ’s momentum dependence between quasiparticles at different positions in the Brillouin zone. For those at (π, 0) or (0, π), the momentum dependence is dominated by nearest-neighbor correlations. For those at (π/2, ±π/2), the momentum dependence is quite one-dimensional. It is an important future study to clarify how to relate these exotic correlations to properties of conductivity.

This work is collaboration with Toshihiro Sato at RIKEN.

References

• [1] T. Sato, K. Hattori, and H. Tsunetsugu, Phys. Rev. B 86, 235137 (2012); J. Phys. Soc. Jpn. 81, 083703 (2012).

Authors

• H. Tsunetsugu