In strongly correlated electrons systems, many exotic phenomena such as high-T_c superconductivities have been found. To clarify how the strongly electronic correlations induce such exotic phenomena, highly-accurate numerical methods for the low-energy effective models of strongly correlated electron systems such as Hubbard model play essential role. For the ground-state calculations (zero-temperature calculations), powerful numerical algorithms such as density matrix renormalization group method or tensor network algorithms already exist and they have been applied to broad range of the strongly correlated electrons systems. However, for the finite-temperature calculations, the efficient numerical method is absent and development of highly-accurate finite-temperature calculations remains a challenging problem.

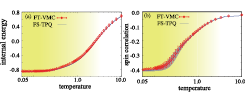
Fig. 1. (a) Temperature dependence of internal energy per site calculated from FT-VMC for 4×4 half-filled Hubbard model with U/t=4. The FT-VMC result is shown by red circles in comparison with essentially exact results obtained by full-space TPQ (FS-TPQ) method shown by blue curve. (b) Temperature dependence of nearest neighbor spin correlations calculated by FT-VMC (red circle) and FS-TPQ (blue curve) method. The shadow region in (a) and (b) represent the error bars in FS-TPQ method.

In the textbook implementation of the finite-temperature calculation, it is necessary to take ensemble average over the excited states and it is practically formidable to carry out. Contrary to the standard implementation, recent development of the statistical physics shows that the calculation within small number of pure states instead of the full ensemble average is sufficient for accurate estimate of finite-temperature properties. Such pure states are called thermal pure quantum (TPQ) states and they are easily generated by performing the imaginary-time evolution of the wave function.

Based on the principle of the TPQ, we develop a new method to perform the calculations for the larger system size where the exact imaginary-time evolution is impossible. A key fact is that accurate imaginary-time evolution of the wave functions is possible by using the stochastic reconfiguration method, which is used as the optimization method in the variational Monte Carlo (VMC) method. Thus, we call this numerical method finite-temperature VMC (FT-VMC) method. By comparing the exact results, as shown in Fig. 1, we have shown that temperature dependence of the physical properties such as internal energy and spin correlations is well reproduced by using the FT-VMC method. Moreover, we have shown that our method can be applicable to larger system size where the exact imaginary-time evolution is impossible. Our method opens a new way for the accurate calculations of the strongly correlated electron systems.

References

• [1] K. Takai, K. Ido, T. Misawa, Y. Yamaji, and M. Imada, J. Phys. Soc. Jpn. 85, 034601 (2016).

Authors

• K. Takai^a, K. Ido^a, T. Misawa, Y. Yamaji^a, and M. Imada^a
• ^aUniversity of Tokyo