Quantum Transport of Dirac Fermions Coupled with Magnetic Order in EuMnBi2
H. Sakai, M. Tokunaga, and S. Ishiwata
Dirac materials, characterised by linear energy-momentum dispersion near Fermi level, have attracted much attention for their unique transport properties such as half-integer quantum Hall effect, observable even at room temperature in graphene. To expand potential application of their distinct quantum transport, it is highly desirable to control the conduction of Dirac fermions by magnetic moments in solids as well as external fields. Despite recent discoveries of a number of new bulk Dirac materials, quantum transport features have been elucidated mostly in nonmagnetic materials, as exemplified by so-called Dirac/Weyl semimetals, such as Cd3As2, Na3Bi, and TaAs.
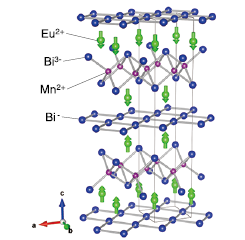
Fig. 1. Schematic illustration of the crystal and magnetic structure for EuMnBi2 at zero field, together with the formal valence of each ion. The magnetic moments of the Mn sublattice are not shown for brevity.
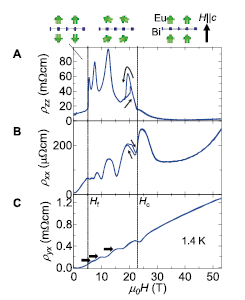
Fig. 2. Field profile of (A) interlayer resistivity ρzz, (B) in-plane resistivity ρxx, and (C) Hall resistivity ρyx for EuMnBi2 at 1.4 K for the field parallel to the c axis. Schematic illustration of variation of the ordered Eu moments adjacent to the Bi layer is presented above the panels.
We here report novel magneto-transport features for a new multilayer Dirac fermion system EuMnBi2. Recently, layered magnets AMnBi2 (A=Sr2+ [1-3] and Eu2+ [4,5]) were found to host anisotropic 2D Dirac fermion, providing an ideal arena to reveal the interplay between Dirac fermions and ordered magnetic moments. The crystal structure consists of the conducting layers of Bi square net hosting quasi two-dimensional (2D) Dirac fermions and the insulating magnetic layers consisting of the Mn-Bi and A layers (Fig. 1). To explore quantum transport phenomena associated with magnetically-controllable Dirac fermions, we have investigated the detailed magnetic and transport properties by applying field up to 55 T at the International MegaGauss Science Laboratory at the Institute for Solid State Physics [6].
The magnetization dominated by the Eu sublattice shows typical behaviour of uniaxial antiferromagnet. We observed a spin-flop transition for the field of ~ 5.5 T (Hf) along the c axis, followed by saturation at ~ 22 T (Hc) with a saturation moment of ~ 6.5 μB/f.u (not shown here), which reflects the full moment of localised Eu 4f electrons. The in-plane resistivity (ρxx) and interlayer resistivity (ρzz) exhibit clear anomalies at the magnetic phase transition of Eu sublattice (Fig. 2). In particular, ρzz exhibits a large jump at Hf, followed by giant Shubnikov–de Haas (SdH) oscillations that reach ∆ρzz/ρzz ~ 50% in the spin-flop antiferromagnetic (AFM) phase (Fig. 2A). This high ρzz state is terminated at Hc, above which the ρzz value is substantially reduced. Interestingly, the magnitude of the SdH oscillations in ρxx and ρyx (Hall resistivity) is also enhanced in the spin-flop AFM phase (Fig. 2B and 2C), which evolves to plateau-like structures in the ρyx profile as indicated horizontal thick arrows in Fig. 2C. This signifies the first observation of the multilayer quantum Hall effect of quasi 2D Dirac fermions in a bulk magnet [6].
In spite of the strong coupling between the magnetism and transport properties, the carrier mobility is estimated to be as high as µ ~ 14,000 cm2/Vs at 2 K. This indicates that the interlayer conduction is suppressed by the staggered Eu moments along the c axis, whereas the ferromagnetic order within the plane may promote the in-plane transport. Thus, the crystal structure of EuMnBi2 can be regarded as a natural spin-valve structure embedded in a multilayer Dirac fermion system. Our discovery would open the door for engineering the Dirac fermion transport in magnetic materials suitable for novel spintronic devices with an extremely high speed.
References
- [1] J. Park, G. Lee, F. Wolff-Fabris, Y. Y. Koh, M. J. Eom, Y. K. Kim, M. A. Farhan, Y. J. Jo, C. Kim, J. H. Shim, and J. S. Kim, Phys. Rev. Lett. 107, 126402 (2011).
- [2] J. K. Wang, L. L. Zhao, Q. Yin, G. Kotliar, M. S. Kim, M. C. Aronson, and E. Morosan, Phys. Rev. B 84, 064428 (2011).
- [3] K. Wang, D. Graf, H. Lei, S. W. Tozer, and C. Petrovic, Phys. Rev. B 84, 220401(R) (2011).
- [4] A. F. May, M. A. McGuire, and B. C. Sales., Phys. Rev. B 90, 075109 (2014).
- [5] S. Borisenko, D. Evtushinsky, Q. Gibson, A. Yaresko, T. Kim, M. N. Ali, B. Buechner, M. Hoesch, and R. J. Cava, arXiv: 15070.04847 (2015).
- [6] H. Masuda, H. Sakai, M. Tokunaga, Y. Yamasaki, A. Miyake, J. Shiogai, S. Nakamura, S. Awaji, A. Tsukazaki, H. Nakao, Y. Murakami, T.-h. Arima, Y. Tokura, and S. Ishiwata, Sci. Adv. 2, e1501117 (2016).
