We report our recent studies on correlated topological insulators using ISSP supercomputer. We first investigate a topological Mott insulator in one dimension (1D) to discuss how the edge Mott states emerge due to the interplay of topology and correlation [1]. We then address how the topological state is restored by the temperature in the presence of strong correlations in two dimensions (2D) [2]. We demonstrate that such restoration of topological properties is rather generic, by exploring another correlated topological insulator [3]. We also mention some issues related to topological insulators [4-6].

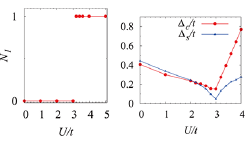
Fig. 1. Left panel: winding number N₁, Right panel: spectral gaps for edge states:Δ_c, (Δ_s) for the one-particle (spin excitation) spectrum [1], as a function of Hubbard interaction U (t denotes nearest neighbor hopping). It is seen that the topological phase transition occurs, but Δ_c does not vanish in contrast to a noninteracting topological transition. Instead, we see the gap closing for collective spin excitations Δ_s.

(A) We first summarize the results obtained for a 1D topological Mott insulator [1]. By examining the bulk topological invariant and the entanglement spectrum of a correlated Su-Schrieffer-Heeger model, we clarify how gapless edge states in a non-interacting topological band insulator evolve into spinon edge states in a topological Mott insulator. Furthermore, we propose a new type of topological Mott transition. In Fig.1, we show a topological Mott transition driven by the Hubbard interaction U [1]. As seen from left panel, a transition from a trivial phase (N₁=0) to a nontrivial one (N₁=1) occurs, and at this transition a one-particle gap (Δ_c) is not closed but only a spin excitation gap (Δ_s) becomes gapless (right panel). This unconventional transition occurs in a spin liquid phase and is accompanied by zeros of the single-particle Green's function and a gap closing in the spin excitation spectrum [1].

(B) We elucidate how a topologically nontrivial phase evolves at finite temperatures [2,3]. Specifically, we study a Kane-Mele Kondo lattice model at finite temperatures with dynamical mean field theory. The obtained phase diagram shows three phases at zero temperature [2]: an antiferromagnetic topological insulator, an antiferromagnetic trivial insulator, and a trivial Kondo insulator. We find a restoration of topological properties at finite temperatures due to the interplay of a topologically nontrivial structure and electron correlation. In order to address this phenomenon, we analyze the bulk and edge properties. In the bulk, the spin-Hall conductivity which is almost zero around zero temperature increases with increasing temperature. At the edge, the gapless edge modes emerge with increasing temperature.

(C) We finally summarize some issues related to topological phase transitions, which will be realized in new platforms such as cold atomic systems, photonic systems, etc. We clarify non-equilibrium topological phase transitions in 2D optical lattices [4]. We unveil hidden topological phases in a 1D quantum walk [5]. We clarify topological properties of cold bosons in 1D quasiperiodic optical lattices [6].

References

• [1] T. Yoshida, R. Peters, S. Fujimoto, and N. Kawakami, Phys. Rev. Lett. 112, 196404 (2014).
• [2] T. Yoshida, R. Peters, and N. Kawakami, Phys. Rev. B 93, 045138 (2016) .
• [3] T. Yoshida and N. Kawakami, arXiv:1604.00122.
• [4] M. Nakagawa and N. Kawakami, Phys. Rev. A 89, 013627 (2014); Phys. Rev. Lett. 115, 165303 (2015).
• [5] H. Obuse, J. K. Asboth, Y. Nishimura, and N. Kawakami, Phys. Rev. B 92, 045424 (2015).
• [6] F. Matsuda, M. Tezuka, and N. Kawakami, J. Phys. Soc. Jpn. 83, 083707 (2014) .

Authors

• N. Kawakami^a, T. Yoshida^a, R. Peters^a, N. Nakagawa^a, F. Matsuda^a, M.Tezuka^a, Y. Nishimura^a, S. Fujimoto^b, H.Obuse^c, and J. K. Asboth^d
• ^aKyoto University of Tokushima
• ^bOsaka University
• ^cHokkaido University
• ^dWigner Research Center, Hungary