Among the triangular lattice antiferromagnets, hexagonal CsCuCl₃ has been studied for a long time because of its interesting crystal and magnetic structures, and magnetic field induced phenomena. Owing to the Jahn-Teller distortion, Cu chains along the c axis are displaced helically in the triangular ab plane and form helices with a six-ion periodicity. This distortion makes the Dzyaloshinskii-Moriya (DM) interaction active with the D vector pointing to the c axis. The S = 1/2 spins of Cu²⁺ ions are ferromagnetically and antiferromagnetically coupled within and between the helical chains, respectively. The competition of ferromagnetic exchange and DM interaction induces the helical spin configuration with an incommensurate (IC) magnetic propagation vector (1/3, 1/3, δ = 0.085) below T_N ~ 10.7 K at zero field, in which spins lie on the triangular ab plane [1]. The magnetic field (H) applied normal to the c axis induces a plateau-like behavior in magnetization between 10.5 and 14.5 T before the spin saturation at 30 T, while for H // c axis magnetization shows a jump at 12.5 T [2]. With increasing H ⊥ c, the IC wave number δ decreases to ~ 0.05 at the beginning of the plateau [IC1 phase in Fig. 1(a)], remains constant in the plateau region (IC3), and decreases to zero on entering a commensurate (C) phase [3]. Using a pulse magnet developed at ISSP, we discovered a new multiferroic (MF) phase and discussed the origin of the emergence of the electric polarization in the chiral magnet CsCuCl₃ [4].

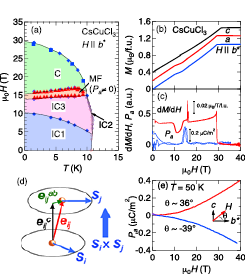
Fig. 1. (a) Magnetoelectric phase diagram of CsCuCl₃ in the H_b*-T plane. (b) Magnetic field (H) dependence of magnetization (M) of CsCuCl₃ for H parallel to the a, b*, and c axes at 1.4 K. (c) H dependence of dM/dH and electric polarization along the a axis, P_a, of CsCuCl₃ for H // b* at 1.4 K. (d) Schematic of the two nearest interlayer Cu ions (spheres). Two adjacent spins S_i and S_j are connected with a unit vector e_ij. (e) P_a(H) curves for the H angle θ ~ –39° and ~ 36° in the paramagnetic region T = 50 K.

Figure 1(b) represents the magnetization (M) of CsCuCl₃ at 1.4 K as a function of H applied along the a, b* and c axes, where b* is perpendicular to the ac plane. In addition to the reported anomalies, we newly observe a jump of M above the plateau region for H // a or b* axis, which is clearly seen as a sharp peak in the dM/dH curve in Fig. 1(c). This field corresponds to the phase transition to the C phase. The most intriguing observation is that the electric polarization along the a axis (Pa) becomes finite just above the IC3 phase and disappears in the C phase for H || b*, as shown in Fig. 1(c). The induced P is as small as ~ 0.25 μC/m². Figure 1(a) is the magnetoelectric phase diagram for the H_b*-T plane. The MF phase is located at H between the upper bound of the M plateau and the lower bound of the C phase. According to a classical calculation [5], spins in each chain are expected to form a chiral soliton lattice in this field region. Observation of higher harmonics in neutron diffraction supports this theoretical prediction [6]. The chiral soliton lattice state comes to attract considerable attention after its discovery in metallic CrNb₃S₆ that belongs to the same point group (622) as that of CsCuCl₃ [7]. The present insulating material exhibits finite electric polarization in the relevant field region. The helical arrangement of Cu ions results in finite local electric polarization normal to the c axis through the spin current mechanism even in the proper screw-type spin order because of the non-zero e_ij × (S_i × S_j) term as shown in Fig. 1(d) [4]. This local polarization will be cancelled out if the helical spin arrangement is incommensurate with the lattice period. In the soliton lattice state, however, distance between the spin helices (solitons) becomes extremely large, and as a result, a small perturbation like magnetoelectric effects of the second order may align the local electric polarization to one direction. This second order effect, which is called as a paramagnetoelectric effect, is actually resolved by our accurate high-field experiments of the magnetoelectric effects in the paramagnetic phase as shown in Fig. 1(e). The emergence of electric polarization is thus explained by the cooperation of the local electric polarization on the chiral solitonic spin arrangement and the paramagnetoelectric effect. Therefore, we interpret this MF phase in CsCuCl₃ as the polar solitonic phase [4].

References

• [1] K. Adachi et al., J. Phys. Soc. Jpn. 49, 545 (1980).
• [2] H. Nojiri et al., J. Phys. (Paris) 49, C8-1459 (1988).
• [3] H. Nojiri et al., Physica B 241-243, 210 (1998).
• [4] A. Miyake et al., Phys. Rev. B 92, 100406(R) (2015).
• [5] A. E. Jacobs et al., J. Phys. Soc. Jpn. 62, 4066 (1993).
• [6] N. Stüβer et al., Physica B 350, e47 (2004).
• [7] Y. Togawa et al., Phys. Rev. Lett. 108, 107202 (2012).

Authors

• A. Miyake, J. Shibuya, M. Akaki^a, H. Tanaka^b and M. Tokunaga
• ^aThe University of Tokyo and Osaka University
• ^bTokyo Institute of Technology