Identification of the gap structure of anisotropic superconductors (SCs) has been the subject of intensive study over many years. Among various experimental techniques, the heat capacity (C_ϕ) measurement in a rotating magnetic field (H) is quite useful because of its wide applicability. This technique is based on the fact that the field-induced zero-energy density of states, N(E=0), in the superconducting mixed state of a nodal SC is field and its orientation dependent. In the case of a tetragonal SC with vertical line nodes, in particular, C_ϕ shows an angular oscillation when H is rotated in the basal plane, with C_ϕ minima occurring along the nodal directions.

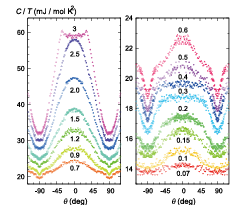
Fig. 1. Polar angle dependence of C/T of URu₂Si₂ measured at 0.2 K in various magnetic fields ranging from 0.07 to 3 T.

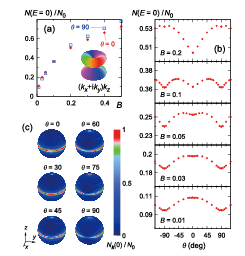
Fig. 2. (a) Field dependence of N(E=0) for B||z and B||x, obtained by microscopic calculations assuming the k_z(k_x+ik_y) gap. (b) Calculated polar angle variation of N(E=0) at several fields. (c) Angle-resolved density of states, N_k(0), mapped on the spherical Fermi surface. The magnetic field is rotated in the xz plane.

To probe the horizontal line node, however, is not so easy. When H is rotated in the ac plane of the tetragonal crystal, the polar angle (θ) variation of the heat capacity C_ϕ(H) is expected to exhibit a twofold oscillation reflecting the gap structure. It should be reminded, however, that because of the tetragonal symmetry of the lattice, the upper critical field H_c2 would have a substantial twofold anisotropy in the ac plane and give rise to a strong twofold background in C_ϕ(H). Hence, the simple argument—the direction of minima in C_ϕ(H) corresponds to the nodal direction—does not hold.

Nevertheless, because the θ variation of the field-induced N(E=0) would exhibit local minima as the direction of H passes through the horizontal line node, fine structures may appear in the twofold oscillation of C_ϕ(H). We applied this technique to the heavy fermion superconductor URu₂Si₂ [1], whose gap structure is suggested by previous experiments to be a chiral d-wave, k_z(k_x+ik_y), having a horizontal line node and polar point nodes [2,3].

Figure 1 shows the measured results of C_θ(H) obtained by rotating H within the ac plane. At high fields, the large twofold oscillation is observed, reflecting the anisotropy of H_c2 predominantly due to the anisotropic Pauli paramagnetic effect. In the low-field region below 0.15 T, no remarkable anomaly was detected in C(θ): the data can be fitted by a simple twofold function expected for an effective mass model. By contrast, a striking feature is found in C(θ) in the region 0.2~1.5 T; a shoulder-like anomaly appears at around θ~45º. With increasing H, this anomaly slightly moves to the higher θ side.

We calculate the θ dependence of the N(E=0) on the basis of the microscopic Eilenberger theory assuming the gap symmetry of k_z(k_x+ik_y) [inset of Fig. 2(a)] and a single-band spherical Fermi surface. For simplicity, the Pauli-paramagnetic effect and the anisotropy of the Fermi velocity are not taken into account. Figure 2(a) shows the field dependence of N(E=0) at θ=0 (H||z) and 90º. For both field directions, H^1/2 dependence is obtained reflecting the line node. Note that a small anisotropy appears in N(E=0).

In Fig. 2(b), N(E=0) is plotted as a function of θ at several fields. The calculated result at a low field B=0.03 can reproduce the features observed in the present experiment, i.e. the shoulder-like anomaly and the dip structure in C(θ) observed at moderate fields. With increasing B, a sharp dip develops at θ=0 and then the anisotropy in N(E=0) is reversed above B∼0.1, reflecting the H_c2 anisotropy. The dip at θ=0 and the reversal of the C(θ) anisotropy in the high-field region, demonstrated in Fig. 2(b), were not detected in the experiment because the actual H_c2 anisotropy depends on the strong Pauli-paramagnetic effect. Figure 2(c) shows the momentum-resolved density of states, N_k(0), mapped on the spherical Fermi surface. The field B=0.03 is rotated in the xz plane. When B||z (θ=0), strong quasiparticle excitations occur on the line node as indicated by a red color. As B rotates towards x direction, the quasiparticle excitations at the region k_y=0 are strongly reduced, resulting in a decrease in N(E=0). This effects account the shoulder-like feature in C(θ) near 45º.

The present results indicate that a horizontal line node exists in URu₂Si₂. Note that among the possible gap structures for a tetragonal even parity SC, only k_z(k_x+ik_y) has the horizontal line node. Thus, the pairing symmetry of URu₂Si₂ is likely to be the chiral d wave [1].

References

• [1] S. Kittaka et al., J. Phys. Soc. Jpn. 85, 033704 (2016).
• [2] Y. Kasahara, T. Iwasawa, H. Shishido, T. Shibauchi, K. Behnia, Y. Haga, T. D. Matsuda, Y. Onuki, M. Siglist, and Y. Matsuda, Phys. Rev. Lett. 99, 116402 (2007).
• [3] K. Yano, T. Sakakibara, T. Tayama, M. Yokoyama, H. Amitsuka, Y. Homma, P. Miranović, M. Ichioka, Y. Tsutsumi, and K. Machida, Phys. Rev. Lett. 100, 017004 (2008).

Authors

• S. Kittaka, Y. Shimizu, T. Sakakibara, Y. Haga^a, E. Yamamoto^a, Y. Onuki^a,b, Y. Tsutsumi^c,d, T. Nomoto^e, H. Ikeda^f, K. Machida^f
• ^aJAEA
• ^bUniversity of Ryukyu
• ^cUniversity of Tokyo
• ^dRIKEN
• ^eKyoto University
• ^fRitsumeikan University