SU(N) Heisenberg Model with Multicolumn Representations
Kawashima Group
Realization of quantum spin liquid in short-range coupling models has been a popular research target in condensed-matter physics for several decades. One approach to obtain a spin liquid state is to consider a Hamiltonian with higher symmetry, which increases quantum fluctuations. Read and Sachdev generalized the antiferromagnetic Heisenberg into SU(N) symmetry [2]. Based on the 1/N expansion they showed that the ground state of the model with sufficiently large N is a valence-bond-solid (VBS) ordering breaking the lattice rotational or the translational symmetry spontaneously. Recently, in the context of the deconfined quantum criticality [3], their theory attracts renewed attention. In particular, the existence of an intermediate state, which might be a spin-liquid state, was discussed near the boundary of Néel and VBS [4,5].
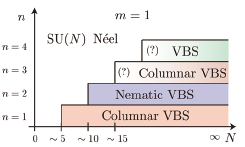
Fig. 1. Schematic phase diagram of the SU(N) Heisenberg model on the square lattice with single-row (m = 1) representations. The phase boundaries for the case of n = 2,3 are determined in the present study. In the case of n = 3,4, we do not see clear evidence of the spontaneous VBS order in the vicinity of the phase boundaries for finite-size QMC simulations.
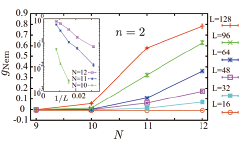
Fig. 2. The Binder cumulant of the nematic order parameter for the model with n = 2 for 16 ≤ L ≤ 128. The inset shows size dependence of the Binder cumulant for N = 10, 11 and 12 in the semi-log scale. The error bars represent the standard errors.
With the famous example of the Haldane gap states, it is now well-known that the nature of the ground state can strongly depend on the representation of the symmetry group even if the symmetry itself is the same. It also applies to the present problem. We consider SU(N) Heisenberg model with the representation of the Young diagram with a single row and n columns. Previously, it was found [4,5] that the Néel state for small N switches to the VBS state for large N without an intermediate spin liquid state. In the case of n = 2, 3, 4, however, though the Néel order disappears at some value of N, no evidence of VBS order has been found in QMC calculation for the L×L square lattice up to L = 32 [5]. At first sight, this result may appear to suggest an intermediate phase between the Néel phase and the VBS phases. In the present work [1], we investigate this problem to clarify whether the intermediate phase exists or not.
First, we examine the case of n = 2. In Fig. 2, we show the Binder parameter of the VBS order parameter for various N and L. The Binder parameter should be 1 when the corresponding order exists and 0 otherwise. From the figure, we see that the VBS order is absent for N = 9 while it exists for N = 11. While the case N = 10 may seem marginal at the first sight, it is approaching the value 1 as can be seen in the inset. From these observations, we conclude that in the case of n = 2 the ground state is the Néel state for N ≤ 9 , while it is the nematic VBS state for N ≥ 10. There is no intermediate phase.
For n = 3 and 4, the problem is harder. In the case of n = 3, while the system size dependence of the Néel order parameter shows that the Néel states end at N = 14, no clear VBS order can be seen in our calculation up to L = 128. To see if this can be regarded as an evidence of the intermediate spin liquid state, we re-examine the prediction of the large-N theory [2], and we find a correspondence between the two cases: (n,N) = (2,10) and (3,15). When the order is small, even if it is finite, the numerical estimate shows apparent 1/L decay for small L regime, and eventually deviates from it. From the known size dependence of the order parameter for the (2,10) case and the correspondence between the two cases, we estimate the cross-over system size at which the size dependence starts to deviate from 1/L behavior in the (3,15) case. It turns out that this cross-over size is around L = 400, indicating that the order is too small to detect even if it exists as the 1/N theory predicts. The situation is similar for the n = 4 case.
To summarize, none of the existing evidence contradict to the absence of the intermediate spin liquid phase, and the absence is confirmed in the n = 2 case while direct confirmation is still missing for larger n.
References
- [1] T. Okubo, K. Harada, J. Lou, and N. Kawashima, Phys. Rev. B 92, 134404 (2015)
- [2] N. Read and S. Sachdev, Phys. Rev. B 42, 4568 (1990); N. Read and S. Sachdev, Nucl. Phys. B 316, 609 (1989).
- [3] T. Senthil, A. Vishwanath, L. Balents, S. Sachdev, and M. P. A. Fisher, Science 303, 1490 (2004).
- [4] K. Harada, N. Kawashima, and M. Troyer, Phys. Rev. Lett. 90, 117203 (2003).
- [5] N. Kawashima and Y. Tanabe, Phys. Rev. Lett. 98, 057202 (2007).
