東京大学高輝度光源計画
加速器の概要
挿入光源の影響と補正
IDの影響の定式化
以下は神谷幸秀先生講義録、および田中均先生講義録のほとんど丸写しに過ぎません。
水平偏光
水平偏光アンジュレーターの磁場は、y 方向の磁場が進行方向 z に対して 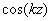 と変化するとおくと、自動的に
と変化するとおくと、自動的に
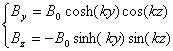 となる。この磁場を運動方程式
となる。この磁場を運動方程式
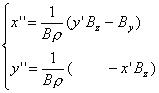 に代入して解く。
に代入して解く。
ここで、アンジュレーターを偏向磁石の連続だと考えると、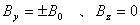 であり、磁場は矩形、中心軌道は円弧の連続となる。(この場合、運動方程式も厳密に解ける。) このことを参考にして、粒子の運動を中心軌道(早い正弦状の運動)とその回りの微小振動(遅い振動、ベータトロン振動)に分けて解くことを考える。すなわち、
であり、磁場は矩形、中心軌道は円弧の連続となる。(この場合、運動方程式も厳密に解ける。) このことを参考にして、粒子の運動を中心軌道(早い正弦状の運動)とその回りの微小振動(遅い振動、ベータトロン振動)に分けて解くことを考える。すなわち、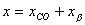 とする。中心軌道として考えるものは、運動方程式の中で
とする。中心軌道として考えるものは、運動方程式の中で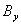 に依存する部分のみを取り出した項
に依存する部分のみを取り出した項
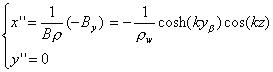 を考えればよい。数学的には、逐次近似法であり、試行解が中心軌道、残渣が微小振動である。これを
z に露わに依存している部分のみ積分し、中心軌道は
を考えればよい。数学的には、逐次近似法であり、試行解が中心軌道、残渣が微小振動である。これを
z に露わに依存している部分のみ積分し、中心軌道は
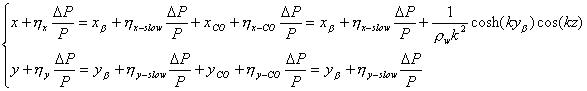
となる。また、中心軌道から発生する分散関数は、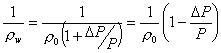 より、中心軌道と逆向きの正弦状に存在する。これを運動方程式に代入し、z
方向に対して平均化を行う。垂直方向の運動方程式は、
より、中心軌道と逆向きの正弦状に存在する。これを運動方程式に代入し、z
方向に対して平均化を行う。垂直方向の運動方程式は、
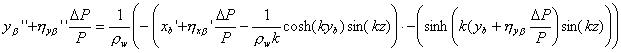 となり、
となり、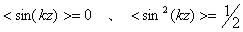 を用い、1次まで取ることにすれば、結局、以下のベータトロン振動の方程式が得られる。
を用い、1次まで取ることにすれば、結局、以下のベータトロン振動の方程式が得られる。
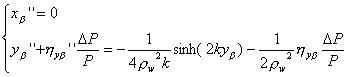
線形化するとベータトロン振動の式も分散関数の式も等しくなり、
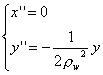 という式になる。これは、x 方向にはドリフトスペースであり、y 方向には集束力が存在することを示している。従って、転送行列は、
という式になる。これは、x 方向にはドリフトスペースであり、y 方向には集束力が存在することを示している。従って、転送行列は、
 となる。実際の計算においては、偏向磁石のエッジフォーカスを使ってこの効果を出している。すなわち、曲率半径
となる。実際の計算においては、偏向磁石のエッジフォーカスを使ってこの効果を出している。すなわち、曲率半径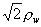 の矩形の磁石を考えると、磁極の内側では、x
方向に
の矩形の磁石を考えると、磁極の内側では、x
方向に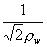 の集束力が加わり、両端では
x 方向に
の集束力が加わり、両端では
x 方向に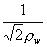 の発散力が、y
方向に
の発散力が、y
方向に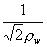 の集束力が加わって、差し引きすると、y
方向のみに集束力が加わり、欲しい効果が得られる。
の集束力が加わって、差し引きすると、y
方向のみに集束力が加わり、欲しい効果が得られる。
円偏光
円偏光アンジュレーターの取り扱いも、同様である。x 方向の磁場を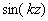 、y
方向の磁場を
、y
方向の磁場を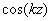 とおくと、磁場は
とおくと、磁場は
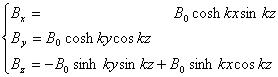
となる。同様に運動を中心軌道とベータトロン振動に分けて、
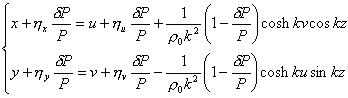 とおく。ただし、ベータトロン振動の部分を
とおく。ただし、ベータトロン振動の部分を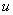 、
、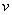 とした。また、この場合、中心軌道は螺旋状であり、x、y
両方向に逆向き螺旋の分散関数が存在している。(すなわち、y 方向のエミッタンスがここで生じる。) これらを運動方程式に代入して解くと、ベータトロン振動の部分は、
とした。また、この場合、中心軌道は螺旋状であり、x、y
両方向に逆向き螺旋の分散関数が存在している。(すなわち、y 方向のエミッタンスがここで生じる。) これらを運動方程式に代入して解くと、ベータトロン振動の部分は、
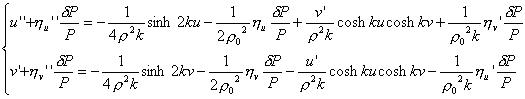 となる。記号を置き換えて、線形化すると、
となる。記号を置き換えて、線形化すると、
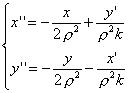 となる。これは、
となる。これは、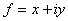 とおいて、減衰振動と同じ形の方程式
とおいて、減衰振動と同じ形の方程式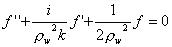 に帰着させて解いて、結局、転送行列は
に帰着させて解いて、結局、転送行列は
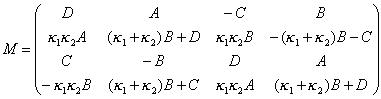 と書ける。ただし、
と書ける。ただし、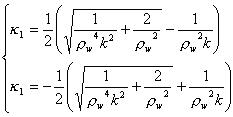 であり、
であり、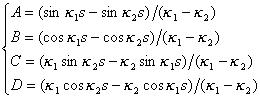 である。
である。
また、トラッキングの際はsymplectic条件より、右辺の運動量として転送前後の平均を取る必要があり、
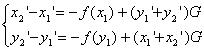 で行うこととなる。ただし、
で行うこととなる。ただし、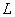 を蹴りの間隔として、
を蹴りの間隔として、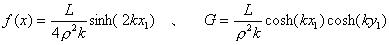 である。これを解いて、
である。これを解いて、
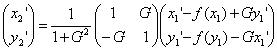 となる。
となる。
Updated on Wednesday,17,Jan.,2001
SOR施設加速器部門
目次へ
軌道放射物性研究施設へ
と変化するとおくと、自動的に
より、中心軌道と逆向きの正弦状に存在する。これを運動方程式に代入し、z
方向に対して平均化を行う。垂直方向の運動方程式は、
、y
方向の磁場を
とおくと、磁場は