軌道補正方法（ＣＯＤ補正）

---

新しい軌道補正方法

新しい軌道補正方法の概念図を示す。

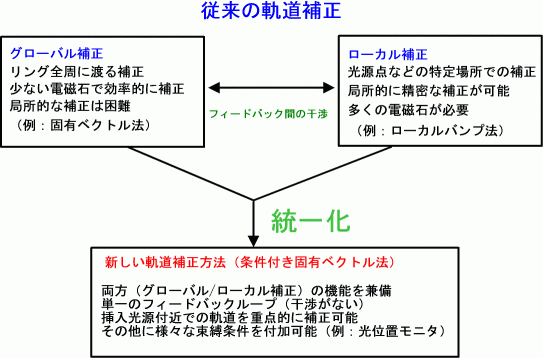
条件付き固有ベクトル法（新しいＣＯＤ補正方法）の定式化

固有ベクトル法（従来の方法）

現在、加速器におけるビーム軌道補正用フィードバックシステムに用いられているCOD補正方法としては、固有ベクトル法、最小二乗法、フーリエ分解法などがある。ここでは、固有ベクトル法について解説する。

いま、BPMで測定したCOD、ステアリングの蹴り角、レスポンスマトリックスをそれぞれ、,, R とする。またBPMの数をＭ個、ステアリングの数をＮ個とすると、レスポンスマトリックスはMxNの行列である。いま、ノルムを(1)式で定義する。

( 1 )

いま(1)が可能な限りゼロに近づくようなを求めることが目的である。ここで、i 番目のBPMにおけるベータトロン関数、位相をそれぞれ、(β_i , Φ_i^B) とし、j 番目のコレクター（ステアリング電磁石）におけるそれらを(β_j , Φ_j^C)と書くことにすれば、レスポンスマトリックスのij 要素は下式のように表せる。

( 2 )

ノルムは、θ_j ( j=1,2,……, N ) に関する微分がゼロになるときに最小値を取る。このとき、ステアリングの蹴り角を表すベクトルは、以下のように決定される。

( 3 )

ここで、”T”は転置行列（或いは、ベクトル）を表す。R^TRは、実対称行列であるから、

( 4 )

と表せる。

U 、Λはそれぞれ以下のように書ける。

( 5 )

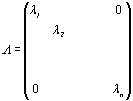( 6 )

ここで、、はそれぞれ,行列R^TRに関するi番目の固有ベクトル、固有値を表す。

式(4-3),(4-4)より、は以下のように得られる。

( 7 )

ここで、

( 8 )

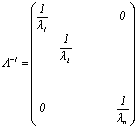( 9 )

である。

ここで小さな値の固有値に関しては、行列Λ^-1において、その逆数をゼロで置き換える。

この操作により、ステアリングが大きな蹴り角を持つことを防ぐとともに、BPM、ステアリングのエラーを緩和することができる。

条件付き固有ベクトル法（新しい方法）

条件付き固有ベクトル法では、固有ベクトル法に束縛条件を付加して解くことになる。ここでの束縛条件とは以下の(10)式で与えられ、ローカルCOD補正の役割をはたす。

（ i=1,………, L ） ( 10 )

ここで、Lは束縛条件の数を表す。いま、(1)式で表されるノルムを(10)式の条件下でラグランジュの未定乗数法を用いて解く。関数S が次式で与えられるとき、

( 11 )

Sの、に関する微分がゼロになるとして、

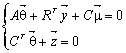( 12 )

を得る。ここで、

, , , ( 13 )

である。前セクションの固有ベクトル法の場合と同様にして、逆行列A^-1はn 個の固有ベクトルを用いて、

( 14 )

と表せる。ここで、(12)の連立方程式を解くことにより、

( 15 )

( 16 )

と得られる。この(16)式が、固有ベクトル法における(7)式に対応するものである。

ここで、

( 17 )

逆行列P^-1が存在するための必要条件は、n≧L である。また、(10) の z_i が任意に選ばれたBPMにおけるビーム位置で、行列Cが選んだBPMに対応したレスポンスマトリックスR の部分行列である場合、選んだBPMでのビーム位置はゼロに束縛される。

例えば、BPMとして挿入光源の両端にあるものが選ばれれば、リング全周に渡るCODを補正しつつ、同時に、挿入光源の両端におけるBPMでのビーム位置と角度もゼロに保つことが可能である。