Quantum phase transitions and related phenomena constitute a field of great interest in the physics of strong correlation. Recently, the Jaynes-Cummings lattice (JCL) attracts much attention in this field, partly because it is a good model system for studying strongly correlated polariton physics and partly because it offers potential use of a quantum simulator for solid-state Hamiltonians, just like the cold-atom systems.

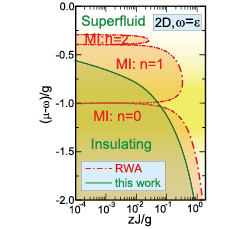
Fig. 1. Phase diagram in the [(μ-ω)/g, zJ/g] space, or the particle average number vs intersite coupling strength J in units of the atom-photon coupling g, for the two-dimensional square JCL at the resonant condition of ω = ε, where z is the coordination number. The inclusion of the usually neglected counter-rotating term makes such a radical change in the phase diagram; in particular, the eminent Mott lobes are eliminated.

The JCL model is composed of a lattice of electromagnetic micro-cavities with frequency ω, each coupled to a two-level atom with level spacing ε, and the intrasite atom-photon coupling g is competed with the intersite photon hopping J. A mean-field treatment of the model reveals a phase transition from Mott insulator (MI) to superfluid phase, resembling in large parts the phase diagram of the Bose-Hubbard model with an eminent feature of the Mott lobes at the boundary between the insulating phase and the superfluid one (See Fig. 1). Both numerical and analytical methods have been employed to study the phase diagram as well as the spectra of low-lying excitations beyond the mean-field approximation and confirmed the existence of the Mott lobes.

All those theoretical studies, however, have not been done on the physically correct original JC model but under the rotating-wave approximation (RWA), in which the Hamiltonian H_RWA commutes with the polariton number operator N_p at each lattice site, leading to the conservation of the local polariton number as specified by the chemical potential μ. This conservation law is, in fact, a key feature to provide the Mott lobes in the phase diagram.

The counter-rotating (CR) term H_CR, included in the original JCL model but neglected so far, will be irrelevant in resonance experiments to detect real transitions, but this will be physically relevant in virtual transitions in the formation of the ground state, making the RWA for the JCL model less reliable in describing the ground-state properties, especially for g of the order of ω and/or ε. Besides, H_CR breaks the conservation of the local polariton number, i.e., [H_CR,N_p] ≠ 0, implying a radical change of the phase diagram, once the CR is included. Moreover, H_CR induces an additional long-range interaction between cavities, enhancing a long-range ordering in the JCL model.

Here we have studied the effects of H_CR on the quantum phase transition of light in the two-dimensional (2D) square JCL with H_CR faithfully included. The ground state as well as spectra of low-lying excitations in both the insulating and the superfluid phases is investigated with use of a sophisticated unitary transformation, which has been developed in the polaron physics. The obtained phase diagram is shown in Fig. 1, indicating that the Mott lobes are absent in sharp contrast with the case of RWA. Thus we may conclude that the physics of the JCL is basically different from that of the Bose-Hubbard model as opposed to the conclusion drawn in the preceding works.

Finally we find that gapped excitations appear even in the superfluid phase in our calculation. Note that for the JCL in the RWA as well as the Bose-Hubbard model, the particle number conservation is broken by the superfluid transition, leading to the gapless bosons according to the Goldstone theorem, but if H_CR is included, the number conservation is broken from the outset, making our system stay outside of the Goldstone theorem. In our superfluid transition, the discrete parity conservation law is broken spontaneously, instead.

References

• [1] H. Zheng and Y. Takada, Phys. Rev. A 84, 043819 (2011).

Authors

• H. Zheng^a and Y. Takada
• ^aShanghai Jiao Tong University